Ray Tracing (1) - 강의 리뷰

들어가며

2024년 봄학기에 컴퓨터 그래픽스 강의를 수강하였다. 과거 2021년에 전공선택 강의였던 그래픽스 강의를 수강신청 했었다가 다른 전공필수 강의들의 로드를 감당할 수 없어서 수강취소를 선택했었다. 하지만 그 이후 담당하시던 교수님이 학교를 떠나시게 되면서 2022년, 2023년에는 강의가 열리지 않았다. 이에 졸업하기 전에 그래픽스 강의를 듣지 못하고 졸업하지 않을까 걱정했었는데 다행히도 2024년에 새로운 교수님께서 그래픽스 강의를 개설하셔서 다행히 듣고 졸업할 수 있게 되었다.

강의는 그래픽스의 기본적인 내용들을 전체적으로 훑는 식의 강의로 진행되었다. 3D Geometry, Viewing Pipeline, Subdivision, Rasterization, Texture, Color 등 컴퓨터 그래픽스를 구성하는 다양한 주제에 대해 배우게 되었다. 여기서 다룬 내용은 추후에 기회가 된다면 글로 작성해보도록 하겠다.

다양한 주제 중에서 가장 인상깊었던 내용은 Ray Tracing 이었다. 어쩌면 당연한 것이 컴퓨터 그래픽을 통해서 실제와 가까운 이미지를 뽑아낸다는 것이 일종의 그래픽스를 배우는 데 있어서 목표라고 생각했기 때문이다. 본 글에서는 그래픽스 강의에서 학습한 Ray Tracing과 관련된 지식들과 Ray Tracing 관련 과제를 진행했던 경험 그리고 이를 개선하기 위해 계획하고 있는 점을 다룰 것이다.

Ray Tracing

Local vs Global Illumination Models

• Local/Direct illumination models
  • A surface point receives light directly from all light sources
• Global illumination models
  • A surface point receives light after the light rays interact with other objects

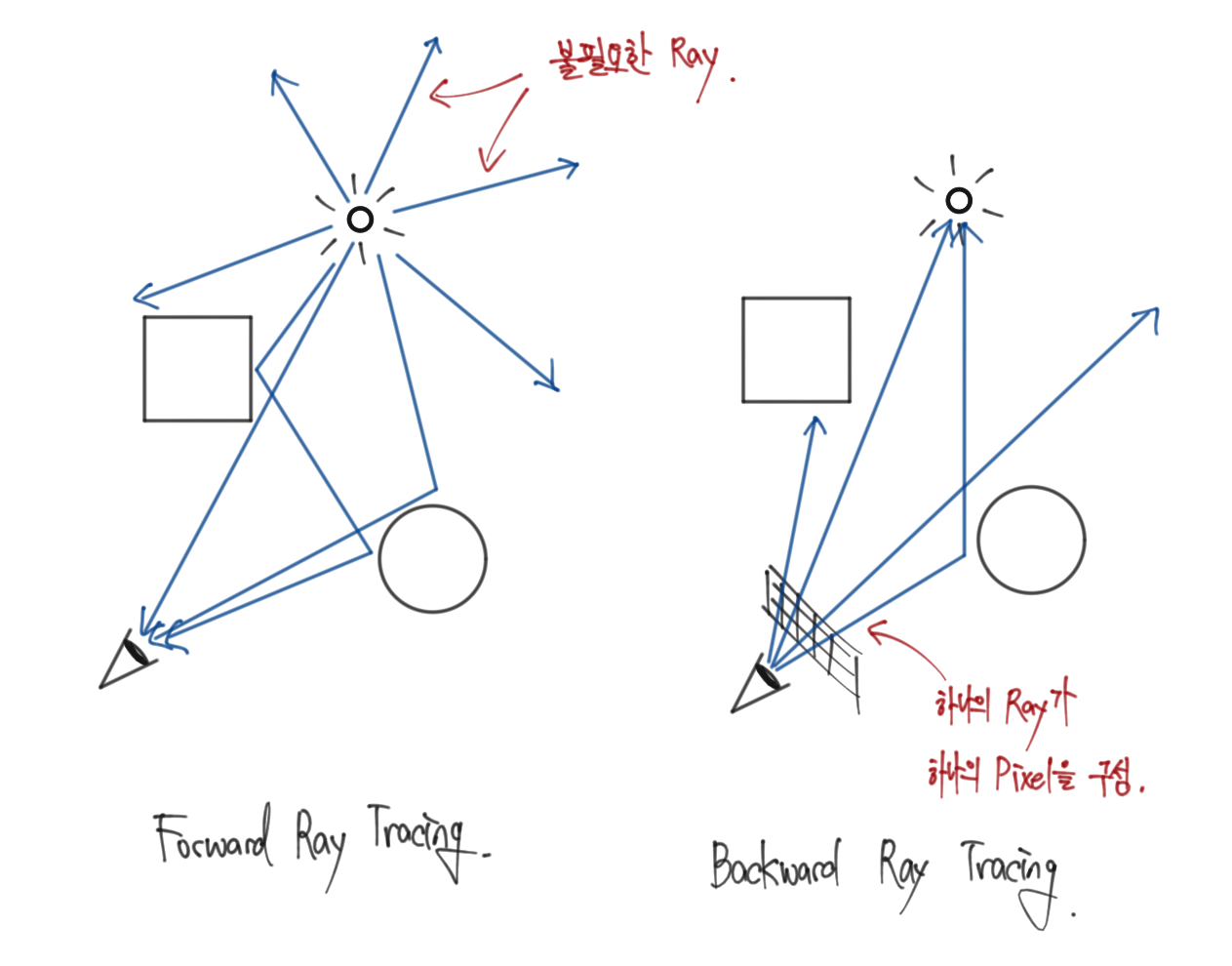
Ray Tracing은 Illumination models를 나누는 두 개의 큰 틀 중에서 Global illumination models 중 하나이다. Ray Tracing은 또 다시 두 개로 나뉜다. 바로 Forward Ray Tracing과 Backward Ray Tracing이다.

Forward/Backward Ray Tracing

Forward Ray Tracing

Forward Ray Tracing은 실제 빛의 작용과 굉장히 유사하다. 광원(Light Sources)에서 여러 Ray를 발사하여 여러 물체에 상호작용한 뒤, 카메라나 인간의 눈으로 들어오는 방식으로 구현하는 것을 말한다. 이는 상술했듯이 실제 빛의 작용과 굉장히 유사하여 직관적인 장점을 가지고 있다. 하지만 광원에서 출발한 Ray가 최종적으로 카메라에 들어가는지 알 수 없기 때문에 무수하게 많은 Ray를 계산해야 해서 컴퓨터로 구현하기에는 무리가 있다.

Backward Ray Tracing

이 문제를 해결한 것이 바로 Backward Ray Tracing이다. Forward Ray Tracing과는 다르게 광원에서 Ray가 출발하는 것이 아닌 카메라 혹은 눈에서 Ray가 출발한다. 300 x 200 이미지를 구성한다고 가정하자. 그렇다면 컴퓨터는 300 x 200 = 60000개의 정량적인 Ray만 계산하면 된다. 따라서 보통 Ray Tracing을 구현한다고 하면 Backward Ray Tracing으로 구현하는 경우가 많다.

구현

Ray Tracing을 구현하기 위해서는 크게 4가지를 구현하면 된다.

1. Local illumination (e.g. Phong illumination model)
2. Shadow
3. Reflection
4. Refraction

이 중에서 Local illumination은 다음 기회에 다루도록 하고 나머지 2, 3 그리고 4번을 다뤄보도록 하겠다. 넘어가기 전에 간단하게 Local illumination을 설명하자면 위에서 언급했듯이 A surface point receives light directly from all light sources. 즉, 빛에 의해서 표면이 얼마나 밝게 표현되는지를 나타내는 개념이다. 따라서 빛을 바라보고 있는 표면은 밝아지고 빛을 등지고 있는 표면은 어두워진다. 더 자세한 내용은 나중에 다뤄보겠다.

(이 때 빛을 바라보고 있는 표면이란 Surface의 Normal Vector를 N, 우리가 주목하고 있는 표면 위의 점에서 광원을 이은 Vector를 L이라고 했을 때, N·L > 0인 표면을 말한다.)

자세한 구현 이전에…

과제 명세

과제로 제출한 코드를 활용하여 설명하기 때문에 전후에 부족한 설명이 있을 수 있다. 자세한 코드는 추후에 Github에 업로드하여 링크할 예정이다.

Precision Problem

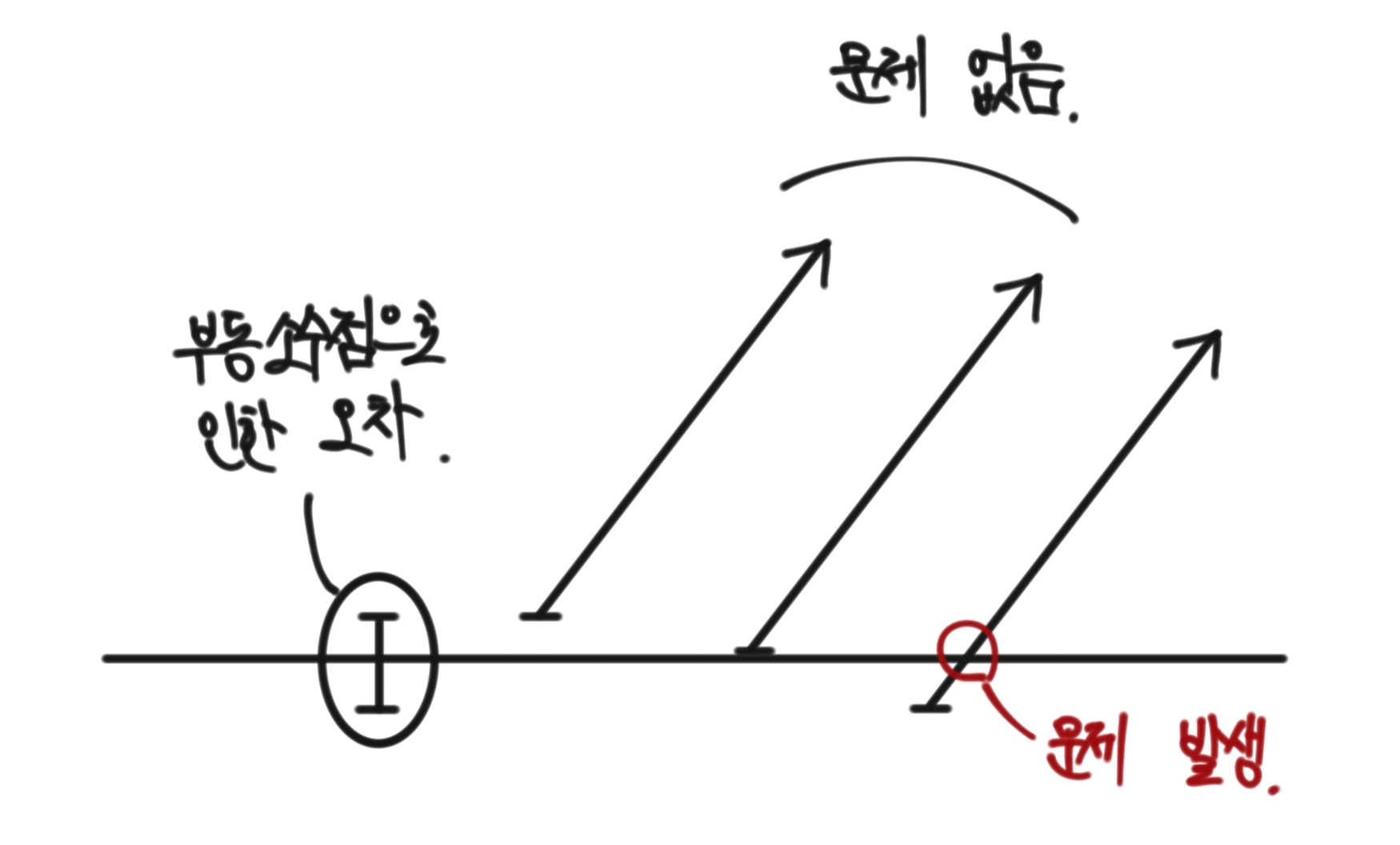
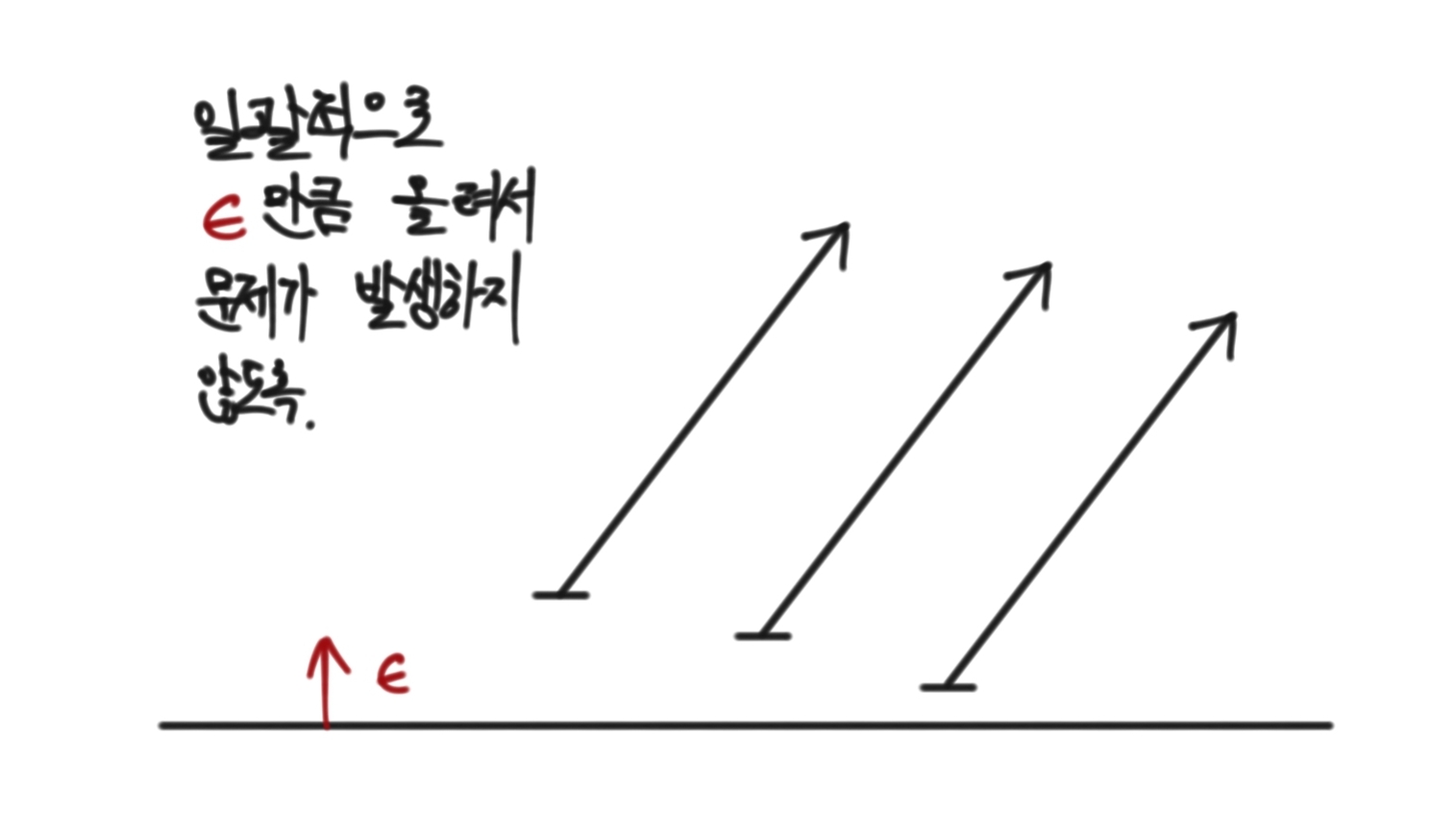
구현 코드를 보다보면 hit_point에서 $\epsilon$만큼 hit_normal 방향으로 이동하여 ray를 만드는 경우를 볼 수 있을 것이다. 이는 컴퓨터에서 실수를 구현하는 방식인 floating point 때문에 발생하는 precision problem을 해결하기 위한 작업인데, hit_point에서 정확하게 ray를 시작할 경우 intersection checking 과정에서 ray를 시작하는 그 물체에 닿아버릴 수 있기 때문이다.

Solve Precision Problem

Shadow

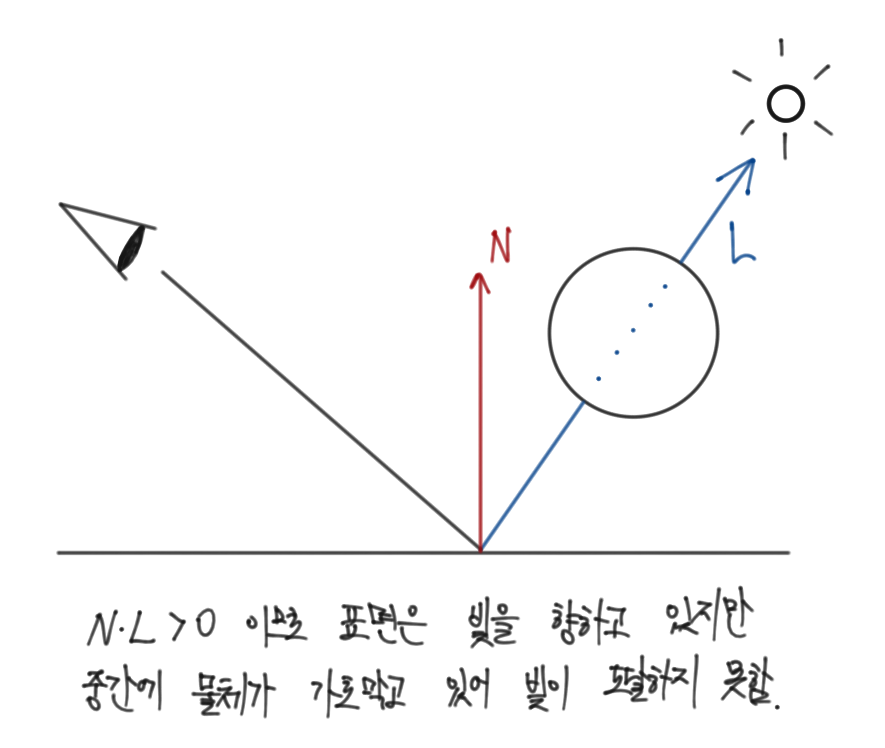
Local illumination 설명을 본다면 Shadow가 구현이 되어있는게 아닌가라는 의문이 들 수 있다. 어느 정도는 맞는 이야기인 것이, 빛을 바라보고 있지 않은 표면은 Local illumination에 의해 어두워지기 떄문에 그림자가 구현되었다고 볼 수 있다. 하지만 여기서 다루는 내용은 Local illumination에서 다루지 않는, 빛을 바라보고 있는 표면이지만 광원과 표면 사이에 물체가 존재하여 빛이 가로막히는 경우를 말한다.

Shadow

이는 다음과 같이 구현할 수 있다.

1. Surface Point로부터 Light까지의 Vector를 구한다.
2. 모든 Entities에 대해 intersection 여부를 확인한다.
3. intersection이 없다면 Local illumination을 적용한다.
4. intersection이 있다면 검은색RGB(0, 0, 0)을 적용한다.

자세한 구현은 다음과 같다.

# For all lights
for light in light_list:
    # L vector
    ray_to_light = Ray(hit_point + 0.001 * hit_normal, normalize(light.pos - hit_point))
    light_dist = np.sqrt(np.dot(light.pos - hit_point, light.pos - hit_point))

    hit2_dist = float('inf')
    hit2_obj = None
    hit2_point = None
    hit2_normal = None

    # Check intersection
    hit2_dist, hit2_obj, hit2_point, hit2_normal = check_intersection(ray_to_light)
    if (hit2_obj is None) or hit2_dist > light_dist:
        # There is no intersection between the surface point and the light
        color += local_shade(hit_obj.color, ray, ray_to_light, light, hit_normal, light_dist)

Reflection

다음은 반사(Reflection)이다.

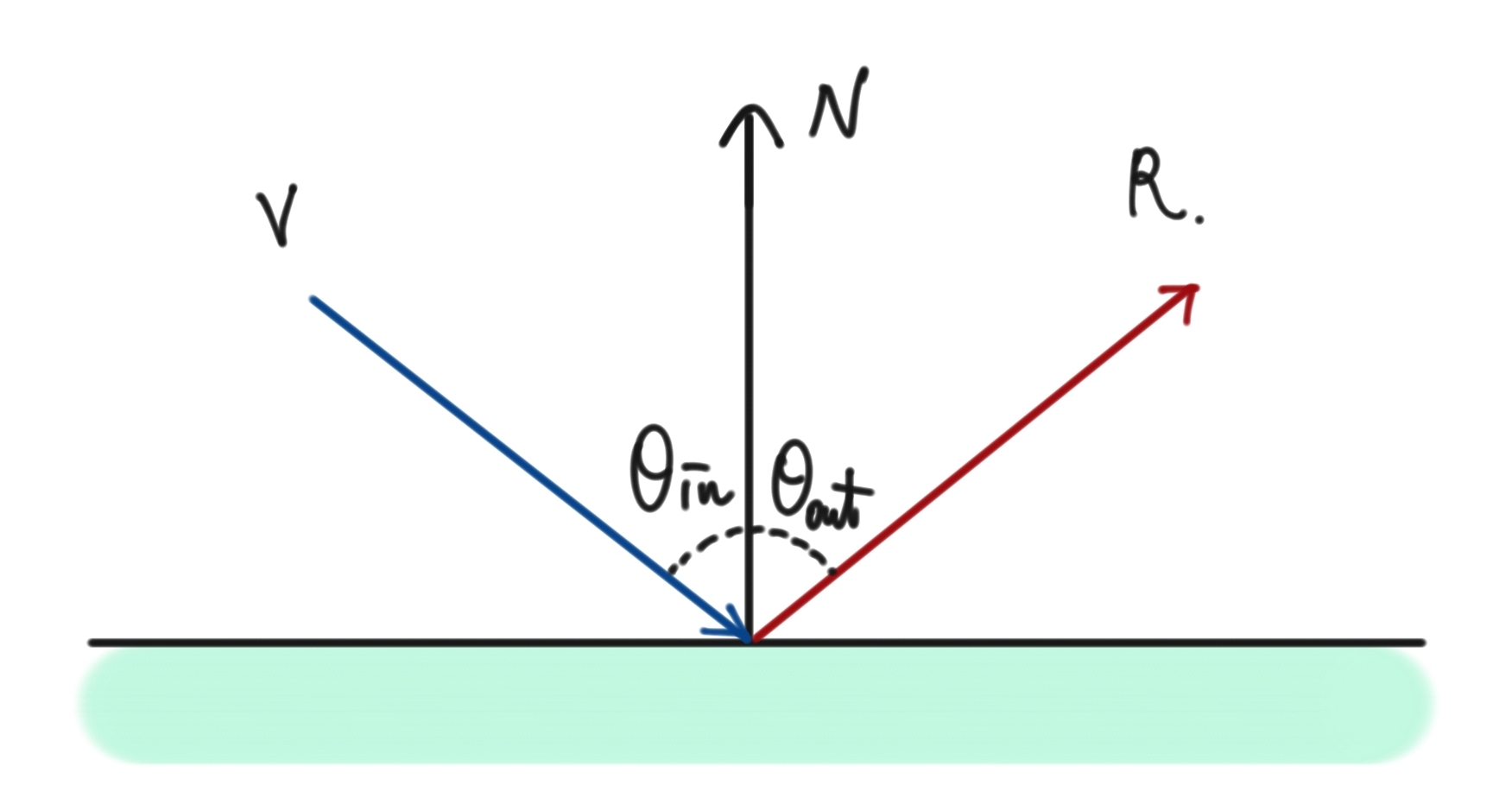
반사의 구현은 현실의 물리법칙을 따른다. 따라서 입사각(angle of incidence) $\theta_{in}$과 반사각(angle of reflection) $\theta_{out}$이 같다.

Reflection

Reflect된 Ray의 color을 얻는 자세한 구현은 다음과 같다.

reflect_dir = normalize(ray.dir + 2 * hit_normal * np.dot(hit_normal, -ray.dir))
reflect_ray = Ray(hit_point + 0.0001 * hit_normal, reflect_dir)
color_reflect = trace_ray(reflect_ray, depth + 1)

Refraction

다음은 굴절(Refraction)이다.

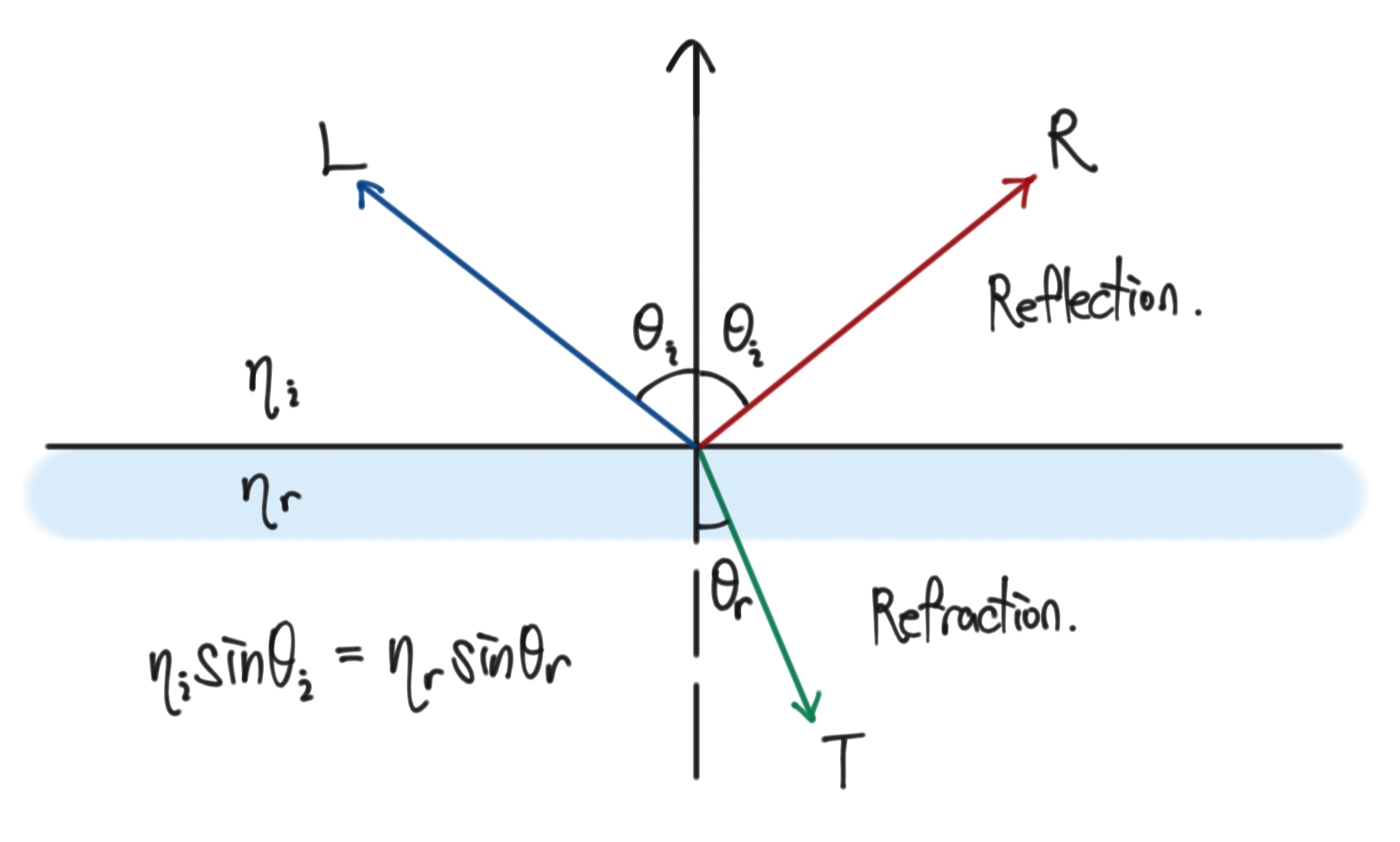
굴절 또한 기존의 물리법칙과 동일하게 구현한다. 스넬의 법칙(Snell’s law)에 따라 굴절 전 매질의 굴절률을 $\eta_{i}$, 굴절 후 매질의 굴절률을 $\eta_{r}$라 했을 때, 입사각(angle of incidence) $\theta_{in}$과 굴절각(angle of refraction) $\theta_{r}$은 다음과 같은 관계를 가진다.

\[\eta_{i} sin{\theta_{i}} = \eta_{r} sin{\theta_{r}}\]

Refraction

굴절을 구현할 때는 여러 상황을 가정하고 구현해야 한다. Shadow나 Reflection은 구현 시에 항상 incident ray가 surface normal 방향에서 들어왔지만 refraction은 surface를 뚫고 나아가는 ray가 만들어지기 때문에 ray가 surface normal의 반대 방향에서 들어오는 경우도 고려해주어야 한다. 또한 스넬의 법칙으로 계산된 $\theta_{r}$이 90도를 넘을 경우 전반사가 일어난다. 따라서 이 경우에는 굴절이 아닌 반사를 적용시켜 주어야 한다.

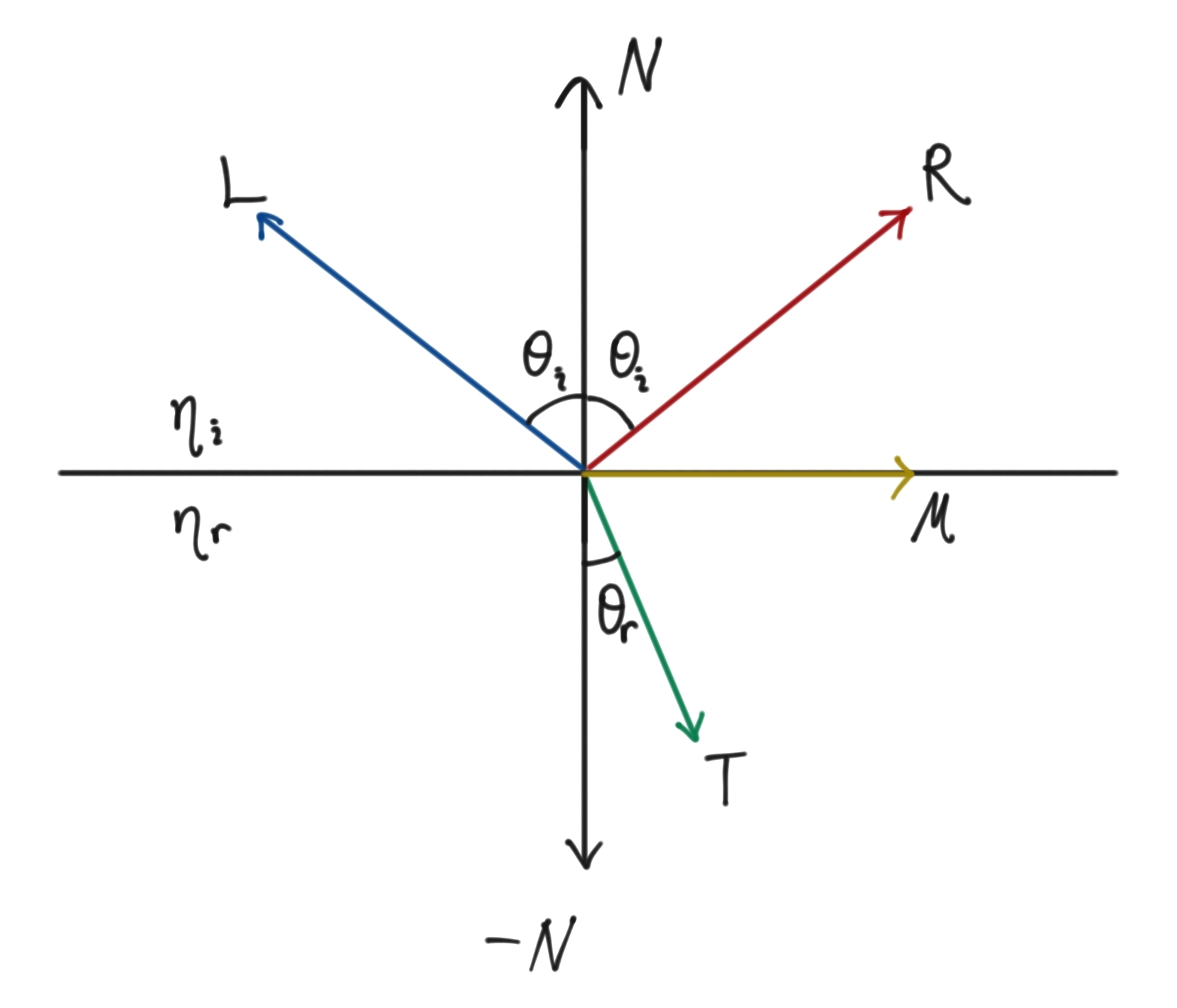
또한 구현 시에 굴절하는 방향인 T는 3차원 상에서 계산되어야 하기 때문에 계산이 복잡하다. 그림을 참고하여 T를 L, N 그리고 $\cos\theta_i$로 나타내는 유도과정은 다음과 같다.

Refracted Direction T

$Let$ $\eta = { {\eta_i} \over {\eta_r} } = $ ${\sin\theta_r} \over {\sin\theta_i}$ , $M={(N{\cos{\theta_i}}-L)\over{\sin{\theta_i}}}$

$Then $

$T=-N\cos\theta_i+M\sin\theta_r$

$=-N\cos\theta_i+(N{\cos{\theta_i}}-L)\sin\theta_r/{\sin{\theta_i}}$

$=-N\cos\theta_i+(N{\cos{\theta_i}}-L)\eta$

$=[\eta\cos\theta_i-\cos\theta_r]N - \eta L$

$=[\eta\cos\theta_i-\sqrt{1-{\sin^2\theta_r}}]N - \eta L$

$=[\eta\cos\theta_i-\sqrt{1-\eta^2{\sin^2\theta_i}}]N - \eta L$

$=[\eta\cos\theta_i-\sqrt{1-\eta^2(1-{\cos^2\theta_i})}]N - \eta L$

이를 바탕으로 한 기본적인 refraction의 구현은 다음과 같다. 이 구현에서는 공기의 굴절률을 1로 가정하고, 반드시 매질 -> 공기 혹은 공기 -> 매질의 상황만 발생한다고 가정하였다.

# hit_obj.ior = eta_r
# therefore, eta = 1 / hit_obj.ior

incident_angle = np.dot(hit_normal, -ray.dir) # cos(eta_i)
refract_dir = (1 / hit_obj.ior * incident_angle - np.sqrt(1 - (1 / (hit_obj.ior ** 2)) * (1 - incident_angle ** 2))) * hit_normal + (1 / hit_obj.ior) * ray.dir
refract_dir = normalize(refract_dir)
refract_ray = Ray(hit_point - 0.0001 * hit_normal, refract_dir, hit_obj.ior)

color_refract = trace_ray(refract_ray, depth + 1)

이 외에도 위에서 서술한 전반사나 매질의 내부에서 공기로 나올 때를 따로 구현해준다.

전반사 확인

incident_angle = np.dot(hit_normal, -ray.dir)
incident_sin = np.sqrt(1 - incident_angle ** 2)
# check total internal reflection
if incident_sin >= 1 / hit_obj.ior:
    ...

매질의 내부에서 공기로 나올 경우

if np.dot(hit_normal, ray.dir) > 0 : 
    ...

추가 구현

Intersection Checking

표면에서 그림자, 반사 그리고 굴절을 구현하였으면 실제로 ray가 물체와 부딫히는지 확인하는 코드를 작성할 필요가 있다. 본 구현에서는 Sphere와 Polygon의 경우에 대해 설명하겠다.

이 때 필요로 하는 값은 ray의 시작 지점에서 부딫힌 point가 ray로부터 얼마나 떨어져 있는지를 나타내는 t값을 구한다. 이 t값을 활용하여 가장 앞에 있는 물체가 무엇인지를 확인한다.

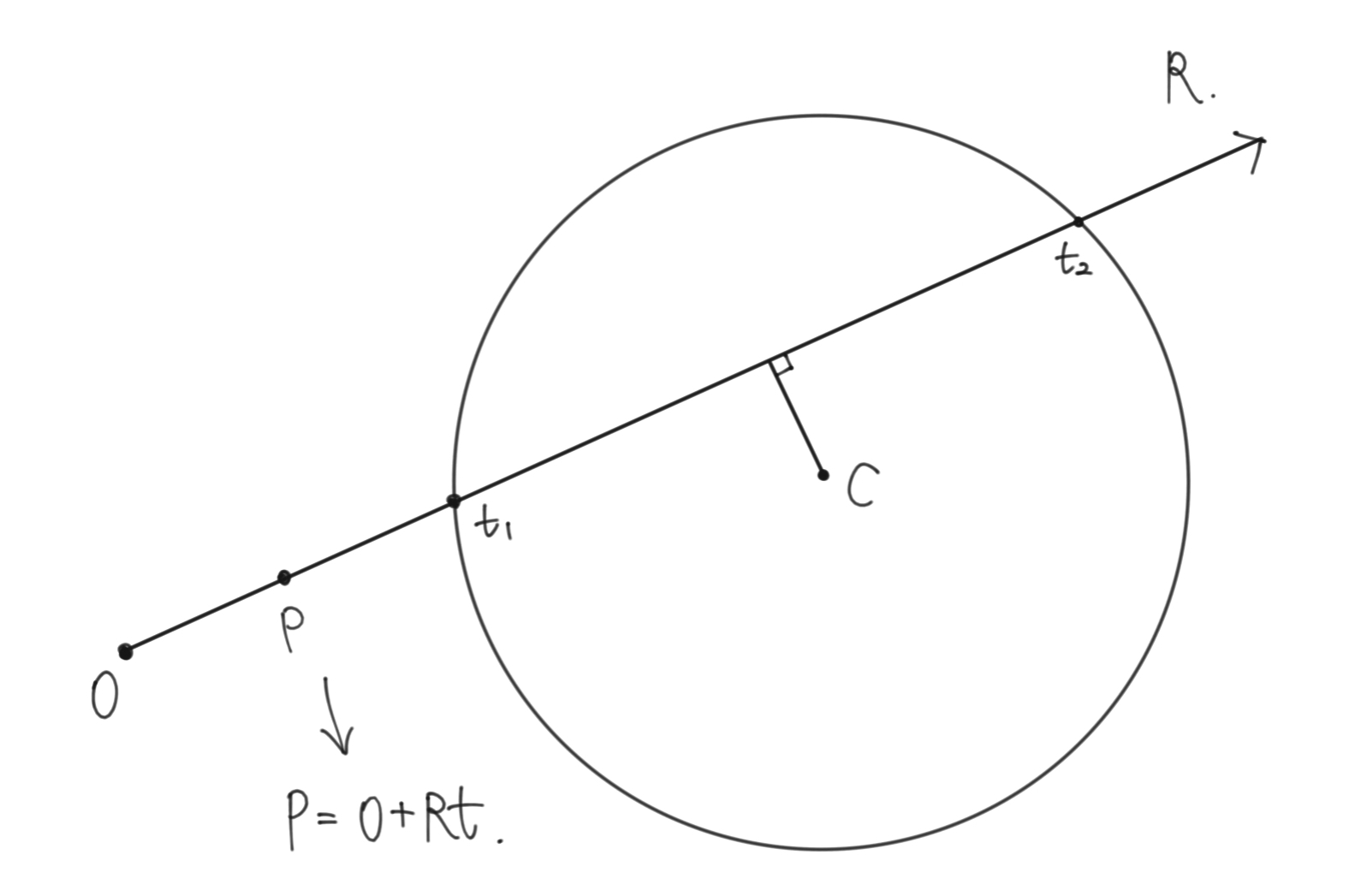
Sphere

Sphere Intersection

$P = O+Rt$

$|P-C|^2 = r^2$

$|P|^2-2P \cdot C+|C|^2=r^2$

$|O|^2+2(O \cdot R)t+|R|^2t^2-2(O+Rt) \cdot C+|C|^2 = r^2$

$|R|^2t^2+2R \cdot (O-C)t+|O-C|^2-r^2=0$

$Let$ $a=|R|^2, b=2R \cdot (O-C), c=|O-C|^2-r^2$

$Then, $ $at^2+bt+c=0$

따라서 t1과 t2를 구하려면 이차방정식을 풀면 된다. 이 중 O에 가까운 값을 사용한다. 이를 코드로 나타내면 다음과 같다.

# class Sphere
def interact(self, ray: Ray):
    oc = ray.orig - self.center
    a = np.dot(ray.dir, ray.dir)
    b = 2.0 * np.dot(oc, ray.dir)
    c = np.dot(oc, oc) - self.radius ** 2
    discriminant = b ** 2 - 4 * a * c
    if discriminant < 0:
        return None
    t1 = (-b - np.sqrt(discriminant)) / (2.0 * a)
    t2 = (-b + np.sqrt(discriminant)) / (2.0 * a)
    return t1 if t1 > 0 else t2 if t2 > 0 else None

Polygon

Polygon의 intersection 구현은 두 부분으로 나눌 수 있다.

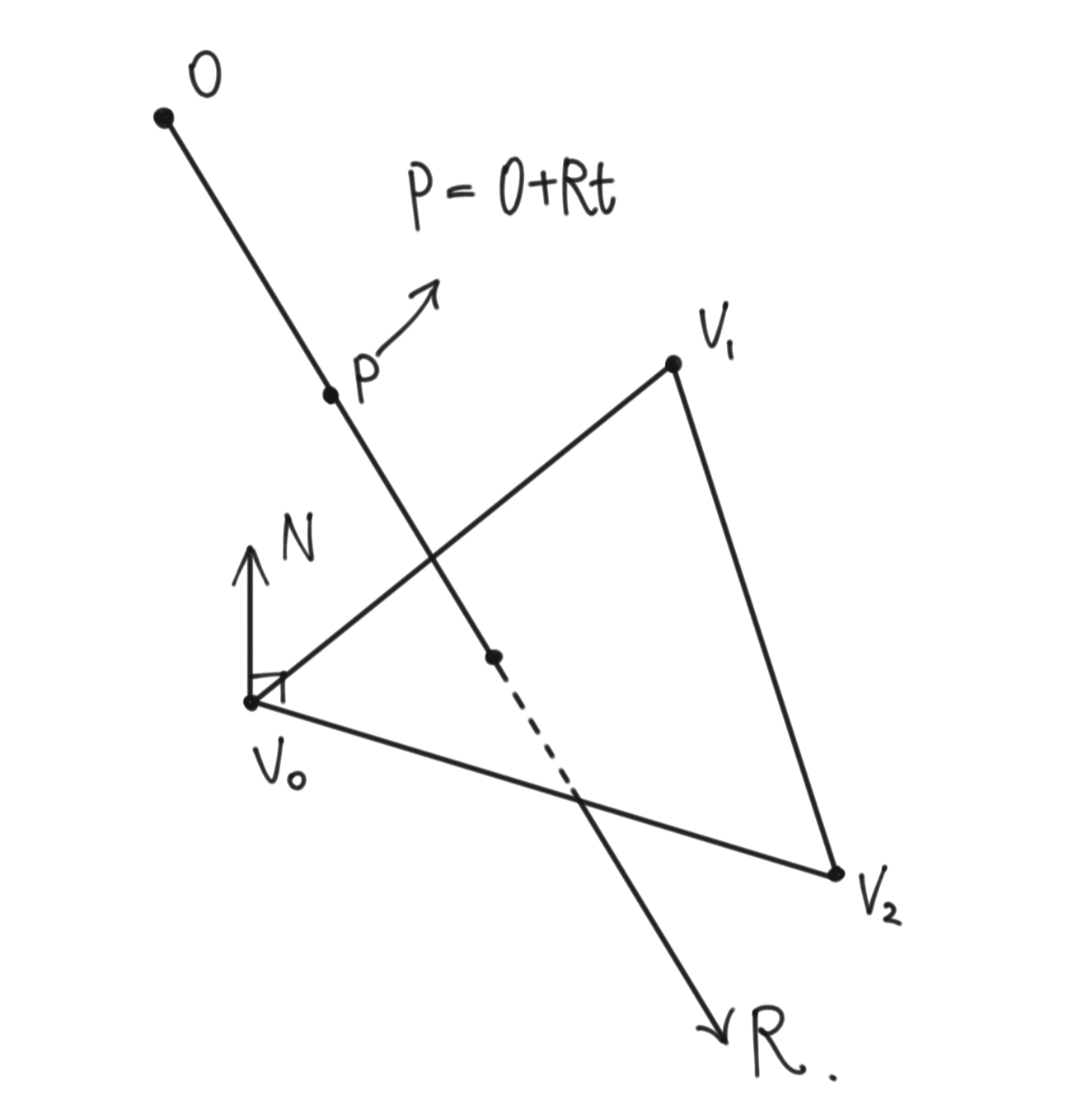
1. Polygon을 포함하는 평면을 ray가 지나는 점 구하기 ($t>0$인 t를 구하기)
2. 그 점이 Polygon을 구성하는 삼각형 안에 있는지 여부 확인

Polygon Intersection

$P = O+Rt$

$N \cdot (P-v_0)= 0$

$N\cdot P = N \cdot v_0$

$N \cdot (O +Rt) = N \cdot v_0$

$N \cdot Rt = N \cdot (v_0 - O)$

$t = {N \cdot (v_0 - O) \over N \cdot R}$

이 과정을 통해 Polygon이 속한 평면 위의 점 P를 구할 수 있다. 이제 P가 실제로 Polygon 위에 있는지를 확인하면 된다. 이는 Barycentric coordinate system을 통해 확인할 수 있다.

간단히 말해서 점 P가 세 점 $v_0$, $v_1$ 그리고 $v_2$가 이루는 평면 위에 있고 $P = uv_0 + vv_1 + wv_2$로 나타낼 때, $u, v, w >= 0$를 만족하면 점 P는 세 점이 이루는 평면 위에 있다는 결론을 내릴 수 있다.

이 전체를 코드로 나타내면 다음과 같다.

# class Polygon
def interact(self, ray: Ray):
    v0 = self.vertices[1] - self.vertices[0]
    v1 = self.vertices[2] - self.vertices[0]
    norm = normalize(np.cross(v0, v1))

    dot_prod = np.dot(norm, ray.dir)

    # The ray does not interact with the polygon
    if np.abs(dot_prod) < 1e-6:
        return None
    
    ov = self.vertices[0] - ray.orig
    t = np.dot(norm, ov) / dot_prod
    if (t <= 0):
        return None

    int_point = ray.orig + t * ray.dir

    u, v, w = barycentric(self.vertices, int_point)

    if (u >= 0) and (v >= 0) and (w >= 0):
        return t
    else:
        # The ray does not interact with the polygon
        return None

결과

결과물

Ray Tracing Result (Cornell Box)

위 조건을 바탕으로 코드를 작성한 결과 성공적으로 결과물을 얻어낼 수 있었다. 가장 가까운 구는 굴절률을 2로 설정한 구이고 그 뒤에 있는 구는 완전 반사가 일어나는 구이다. 그리고 왼쪽 구석에 반사판을 두어 반사 효과가 더 극적으로 보일 수 있도록 설정하였다.

아쉬운 점

과제 조건이 Python으로 구현하는 것이었기 때문에 속도가 너무 느린 것이 단점이었다. 위와같은 장면을 얻기 위해서는 약 10분 이상 기다려야 했으며 cpu multiprocessing을 활용하여 약 5~10배정도 속도를 가속했음에도 불구하고 이와 같은 시간이 걸렸다. GPU를 활용하여 결과를 냈다면 훨씬 빠른 속도로 결과를 얻어낼 수 있었을텐데 과제 기간이 시험기간과 겹치기도 했고 GPU 활용을 단순 모델 학습이 아니라 원하는 계산을 하도록 작업해본 적이 없어서 시간 내에 구현해보지 못했다.

또한 부드러운 그림자를 얻기 위해서는 Point Light이 아니라 Area Light이 필요했는데 과제 명세에서 Point Light을 여러 개 배치하여 Area Light의 효과를 얻어도 인정한다는 내용이 있었다. 그래서 25개의 Point Light을 사용해서 구현하였는데 생각보다 만족스러운 결과를 얻지 못했다.

그리고 수업시간에 다룬 Depth of Field나 Caustics를 구현하지 못한 아쉬움도 있었다. Depth of Field는 우리가 흔히 아는 아웃포커싱이고 Caustics는 위의 결과에서는 굴절 및 반사에 따라 생겨나는 밝은 부분을 뜻한다. 위의 결과물을 예시로 든다면 가장 앞쪽의 구의 그림자 속에 실제로는 빛이 굴절되어 모인 밝은 부분이 생겨나야 하지만 이러한 것이 구현되지 못했다.

목표

일단 Python으로 짜여있는 코드를 C/C++로 옮겨 더 높은 performance를 보이는 환경에서 Ray Tracing을 구현해보고자 한다. 또한 이번에는 GPU까지 활용하여 만족스러운 결과를 더 빠른 속도로 얻을 수 있도록 목표해보고자 한다. 또한 위에서 언급했던 DoF, Caustics를 포함하여 수업 시간에 다룬 더 다양한 Visual Effects를 구현할 것이다.

참고 자료

1. Jungdam Won, Ray Tracing 수업 자료
2. Wikipedia, Refraction, https://en.wikipedia.org/wiki/Refraction
3. Wikipedia, Reflection, https://en.wikipedia.org/wiki/Reflection_(physics)
4. Wikipedia, Barycentric coordinate system, https://en.wikipedia.org/wiki/Barycentric_coordinate_system